Units and measurements

Units & Measurements

Measurements:

A measurement involves comparison of given physical quantity with a standard measuring unit.

For example, for measuring the length of an object we need to compare it with standard length units of 1 meter, 1 foot, etc.

Standard unit:

A standard unit of measurement is a unit that is universally accepted and used for measuring quantities like length, mass, time, etc. These units are fixed and cannot be changed.

System of Units:

(i) CGS: Centimeter Gram Second system

(ii) MKS: Meter Kilogram Second system

(iii) FPS: Foot Pound Second system.

(iv) SI: System International

Fundamental Quantities and Units:

Fundamental quantities: 

The physical quantities which do not depend on any other physical quantities for their measurements are known as fundamental quantities. 

There are seven fundamental quantities

- length, mass, time, temperature, electric current, luminous intensity and amount of substance.

Fundamental units: 

The units used to measure fundamental quantities are called fundamental units.

Derived quantity: 

The physical quantity which depends on fundamental quantities for its measurement are called derived quantities. The derived quantities can be expressed in terms of the fundamental quantities.

Example: Area, Force, Velocity, etc. 

Derived units: 

The units used to measure derived quantities are called derived units.

Supplementary quantities and units:

There are physical quantities which are neither fundamental quantities nor derived quantities, such quantities are called as supplementary quantities and their units are known as supplementary units.

  There are two supplementary physical quantities 

• Plane angle dθ 
• Solid angle dΩ

1. Plane angle (dθ): It is defined for a plane object 

Angle made by a plane arc(curve) at its center is called as plane angle and it is denoted by (dθ).

It is defined as the ratio of length of arc to the radius of an arc.

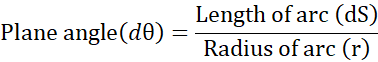
Unit for plane angle is radians or degrees

       180 degrees  = π radians

1. Solid angle (dω): It is defined for solid (3 dimensional) object 

Angle made by a curved surface at its center is called as solid angle and it is denoted by dΩ.

It is defined as the ratio of the area of curved surface to square of radius of the curved surface.

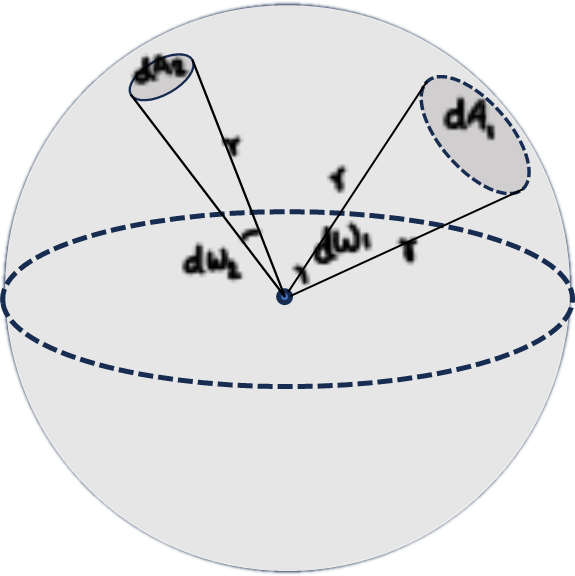
Unit of solid angle is steradian (sr) 

SI units: 

This system is used most widely and accepted worldwide. It uses decimal system, conversion within the system is very simple and convenient.

Conventions for the use of SI Units:

• Unit of every physical quantity should be represented by its symbol.
• Full name of a unit always starts with smaller letter and symbol of unit will be written in capital if it is bases on name of scientist (N for Newton, J for Joules etc.) otherwise in smaller letters.
• Symbols for units always written in singular form (100 N not as 100 Ns).
• Symbols for units do not contain any full stops at the end of recommended letter, e.g., 25 kg and not 25 kg.
• The units of physical quantities in numerator and denominator should be written as one ratio for example the unit of acceleration is m/s2 or m s-2 but not m/s/s.
• Combination of units and symbols for units not used when physical quantity is expressed by combination of two. e.g., The unit J/kg K is correct while joule/kg K is not correct.
• A prefix symbol is used before the symbol of the unit such as  

 1m = 1 milli=10-3

  1μ = 1 micro = 10-6

  1n = 1 nano= 10-9

• Space or hyphen must be introduced while indicating multiplication of two units.

Measurement of length:

• Length is a fundamental quantity; its SI unit of measurement is meter(m).
• One meter is defined as the length of the path travelled by light in vacuum during time of 1/299792458 seconds.
• Measurement of length/distance can be classified into following categories: 

1. Measurement of small length of distance:

• Measurement of small distance or length are done directly by using measuring meter tape, meter scale, vernier caliper or screw gauge etc.

1. Measurement of large distance:

• The measurement of large can not be done directly, therefore it is done by adopting various indirect methods such as:

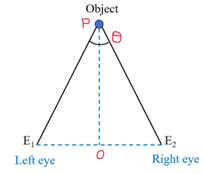
Parallax method: 

When we observe an object through different angle (left eye and right eye), the position of object appears to be changed, it is due to parallax.

Parallax is defined as the apparent change in position of an object due to a change in the position of the observer.

The angle made by two positions of observer with the object is known as angle of parallax (θ).

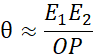
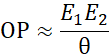
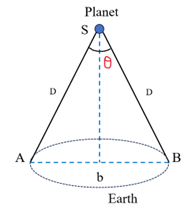
1. Measurement of distance of a planet from Earth:

We select two distant positions on the surface of Earth. The position   A and B separated by a straight line at distance b as shown in Figure.

 Two observers at these two points observe a distant planet simultaneously. We measure the angle ∠ASB between the two directions along which the planet is viewed at these two points. This angle, represented by symbol θ, is the parallax angle.

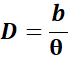
1. Measurement of distance of a star from earth:

As distance of planets from Earth is comparatively very large the parallax angle taken from two distant points on the Earth becomes insignificant.

Earth is revolving around the sun, Hence, the measurement of parallax done when earth is positioned at two extreme points of the orbit around sun. 

The distance between two farthest points along the orbit of the Earth around the Sun is 2AU (AU- Astronomical unit).

Note: 

The astronomical unit (AU): 

It is defined as the mean distance between the center

of the Earth and the center of the Sun.

1 astronomical unit (AU) = 1.496×1011m

A light year (ly): 

It is defined as is the distance travelled by light in one year.

        1 light year = 9.467×1015 m

A parsec (pc): It is defined as the distance from where 1AU subtends an angle of 1 second of arc. 

     1 parsec (pc) = 3.08×1016m ≅ 3.26 light years

1.  Measurement of the size of a planet or a star:

If D is the distance between planet and earth and 𝜶 be the angle between the two directions when two diametrically opposite points of the planet are viewed through a telescope.

Since, the value of D can be found by methods discussed earlier.

We can write,

1. Measurement of very small distance:

To measure very small distance such as a size of the atoms and molecules, etc., the conventional instruments such as vernier calipers or screw gauge will not be useful. Therefore, we use electron microscope or tunnelling electron microscope to measure the size of atoms.

Measurement of Mass:

• Initially in year 1889, A kilogram was defined as the mass of a shiny piece of platinum-iridium alloy kept in a special glass case at the International Bureau of weights and measures.
• The new measure of kilogram is defined in terms of magnitude of electric current required to produce an electromagnet, which can balance weight of standard one kilogram mass. 
• Mass of atoms and molecules are measured in terms of atomic mass units (amu)
• 1amu = 1/12th mass of unexcited atom of C12 isotope of carbon.
• 1amu = 1.6605x10-27 kg

Measurement of time:

• For time measurement, duration of one mean Solar day was considered as reference. 
• A mean Solar day is the average time interval from one noon to the next noon. Average duration of a day is taken as 24 hours.
• One second is defined as 1/86400 of mean solar day.
• It was later observed that the length of a Solar day varies gradually due to the gradual slowing down of the Earth’s rotation.
• Hence to get more standard and non-varying unit for measurement of time, a cesium atomic clock is used.
•  It is based on periodic vibrations produced in cesium atom. In cesium atomic clock, a second is taken as the time needed for 9,192,631,770 vibrations of the radiation (wave) emitted during a transition between two hyperfine states of Cs133 atom.

Dimensional Analysis:

The dimensions of a physical quantity are the powers to which the concerned fundamental units must be raised in order to obtain the unit of the given physical quantity.

For example, If the unit of given physical quantity-X, has index of length as ‘a’ i.e. (length)a, index of mass as ‘b’ i.e. (mass)b and index of time as ‘c’ i.e., (time)c then the dimension of -X is written as:

                                         [X] = [La Mb Tc]

Dimension of velocity:

Dimension of acceleration:

Dimension of force:

Use of dimensional Analysis 

1. To check the correctness of physical equation
2. To establish relationship between related physical quantities. 
3. To find the conversion factor between the units of the same physical quantity in two different systems of units

1. To check the correctness of physical equation:

Each and every term of a correct equation relating various physical quantities must have same dimension.

For example: v= u + at   has same dimension for each term

[v]=[u]=[ut]= [L1 M0 T-1]

1. To establish relationship between related physical quantities. 

It is observed that the time taken by simple pendulum (Period of simple pendulum(T)) changes with change in its length (L) and also the simple pendulum oscillates under the gravitational acceleration(g), Hence we can assume that the period (T), length(L) and gravitational acceleration (g) are related physical quantities.

Hence, we can establish a relation between ‘T’, ‘L’ and ‘g’ by using dimensional analysis.

Let’s assume that the period (T) depends on Length(L) and gravitational acceleration(g).

Hence, we can write,

                                         ………. (1)

Here, K= Dimensionless constant 

For correctness of the above equation, Dimension of each term must be same.

Now,

                                                           …. (1)

                 …. (2)

Equating indices of both the equations (1) & (2),

                                                   a           

Substituting value of a and b in equation (1), We get:

Note:  The value of K can be determined by experiment. In actual practice K= 2π, Hence the actual expression for period is 

1. To find conversion factor for changing unit from one system to another:

Consider the conversion of unit for energy from MKS to CGS system.

The unit for energy in MKS system is joules(J) and in CGS system it is erg.

Let’s assume ‘x’ is the conversion factor for converting joules into ergs.

Therefore, 1 J = x ergs     ---------(1)

The size of fundamental units for L, M and T in both systems will be different, hence the dimensional formula for both systems can be expressed differently.

Let’s assume,

 The dimension of energy in first system is  and the dimension of energy in second system is .

Here suffix-1 indicates MKS system and suffix-2 indicates CGS system.

From equation (1), we can write,

                                      = x

Unit for L1 is meter and that for L2 is centimeter.

Unit for M1 is kilogram and that for M2 is grams.

Also, Unit for T1 and T2 is same i.e. seconds. 

Hence, we can write,

                           …………………. (2)

From equation (1) and (2),

                               1 J =  ergs     

Limitation of dimensional analysis

• The value of dimensionless constant can be obtained with the help of experiments

only.

• Dimensional analysis cannot be used to derive relations involving trigonometric,

exponential, and logarithmic functions as these quantities are dimensionless.

• This method is not useful if constant of proportionality is not a dimensionless

quantity.

For example, we cannot find the expression of gravitational force (F) by dimensional analysis due to the fact that constant of proportionality (G) is not a dimensionless quantity.

                                              unit of G is N-m2/kg2

• If the correct equation contains some more terms of the same dimension, it is not

possible to know about their presence using dimensional equation.

Accuracy:

It is defined as the closeness of measured value of a given physical quantity with its actual value.

For example, if the actual height of given person is 190 centimeters and it is measured by a Scale- A and Scale-B such that both scales give different reading for the height of the person.

Precision:

It is defined as the repetition of the outcome of given measurement.

A precise measurement means multiple measurement of given physical quantity gives same(identical) values. It is known as repetition or reproduction of result.

In measurement, it is always desired to get accurate as well as precise result of measurements.

Uncertainty:

Uncertainty of measurement is the doubt that exists about the result of any measurement.

When any measurement is carried out there exist a certain level of doubt (uncertainty) about the result of measurement.

For example,

If length of a pencil sharpener is measured with the help of measuring scale having least count of 1 mm, any variation of length less than 1 mm cannot be measured by the measuring scale.

 As we can see from the given figure, that the actual length of pencil sharpener is in between 13mm and 14 mm but the scale can only give us reading of 13mm or 14 mm, hence there exist a doubt about the value of measured quantity. This doubt is known as uncertainty of measurement.

In the given example, the doubt in measurement cannot exceed 1mm even if length measured as 13 mm or 14 mm, hence the maximum uncertainty is of 1 mm for this measurement.

Note: 

Uncertainty of measurement is the least count of instrument used for measurement.

Causes of uncertainty:

1) Quality of instrument used.

2) Skill of the person doing the measurement.

3) The method used for measurement.

4) External or internal factors affecting the result of the measurement.

Error:

It is defined as the difference between the actual value of physical quantity and the measured value of physical quantity.

Types of errors:

1. Systematic errors:

The causes of systematic errors can be determined and it can be prevented or reduced by doing proper calibration or improving the method of measurements.

Systematic errors are generally due to faulty instruments or flawed procedures.

Systematic errors can be minimized by using correct instrument, following proper experimental procedure and removing personal error.

The sources of systematic errors:

1. Instrumental errors: This type of error is due to defective instruments used for measurement. If instrument is not calibrated it results into instrumental errors.
2. Imperfect measurement technique: This is an error due to defective setting of an instrument or following wrong procedure of measurement. 
3. Personal error: Such errors are introduced due to fault of the operator, bias of the operator/observer, carelessness in taking observations/readings for measurement etc.

1. Random errors:

These are the errors caused by unknown factors which cannot be eliminated even after following all the procedures to minimize systematic errors. 

These types of errors may be positive or negative.

These errors cannot be eliminated completely but we can minimize them by repeating the same measurement number of times and taking average of all the values(readings) obtained during repeated measurements. 

For example, if length of an object is measured by an instrument, then to eliminate the random error of measurement, the length will be measured number of times such as, L1, L2, L3, L4 ,….,Ln.

The final value of length is given by average of all values obtained during measurement.

Calculation of error:

We know that, 

                        -----------(1)

 Consider a measurement of physical quantity is done. 

The numbers of readings a1, a2, a3, a4 ,…., an are taken to minimize random error of measurement.

Assuming that all precautions are taken to minimize the systematic error.

The most probable value of measurement is given by the mean (average) value of all readings.

Hence, by equation (1), We can find absolute errors in each reading.

Absolute error in a1 =

Absolute error in a2 =

Absolute error in a3 =

Absolute error in aN =

Mean of absolute errors:

Hence, we can write the actual value of ‘a’ in terms of mean of measured values and mean of absolute errors.

  Sign indicates that the error can be positive of negative; The actual value of ‘a’ lies between a and a  .

Relative error:

The relative error is defined as the ration of mean error of measures values to the mean of measured value.

Percentage relative error:

The percentage relative error is given by following expression.

Combination of errors:

When the measurement of a physical quantity (A) depends on the measurement of another physical quantities such as B, C, D, …, etc. The error in the measurement of B, C, D,.. etc.  will be combined to give final error in the measurement of physical quantity ‘A’.

1. Error in addition (sum)

If A = B+C,

Let error in measurement of A, B and C be ±∆A, ±∆B, ±∆C respectively.

)= )+

)= )+

=

There are four possible values of error in A:

1. --------(Maximum)
2. 
3. 
4.  --------(Maximum)

Hence the magnitude of maximum error in measurement of A will be

1. Error in subtraction (difference)

If A = B-C,

Let error in measurement of A, B and C be ±∆A, ±∆B, ±∆C respectively.

)= )-

)= )-

=

There are four possible values of error in A:

1. 
2.  --------(Maximum)
3.  --------(Maximum)
4. 

Hence the magnitude of maximum error in measurement of A will be

(Note: even though A=B-C, the max. error in A will be the sum of error in B and error in C)

1. Error in multiplication (Product):

If A = B x C,

Let error in measurement of A, B and C be ±∆A, ±∆B, ±∆C respectively.

) = ) x

) = 

= 

Since  and  are small, their product will be further small. Therefor  can be neglected.

=  

Hence the magnitude of maximum error in A is given by,

=  

Therefore, the maximum relative error in measurement of A is given by,

1. Error in division (Ratio):

    If ,     

Let error in measurement of A, B and C be ±∆A, ±∆B, ±∆C respectively.

Since  and  are small, their product will be further small.

Therefore, the maximum relative error in measurement of A is given by,

Note: When two quantities are multiplied or divided, their combined relative error is the sum of relative error of individual quantity.

1. Error due to power of measured quantity:

If      

      Hence, the relative error in A is given as,

Similarly, if   we can write relative error in A as,

Similarly, if   we can write relative error in A as,

Significant Figure:

• Significant figures give the meaningful digits in a number obtained during measurement of physical quantity. 
• Significant digit represents the reliable digits in a value, conveying the accuracy of a measurement.
• The number of digits in a measurement about which we are certain, plus one additional digit, the first one about which we are not certain is known as significant figures or significant digits.

For example, if length of a pencil is measured by a scale in centimeters having least count 0.1 cm.

The reading of length taken are 4.3 cm, 4.4 cm, 4.3 cms, 4.3cms and 4.4 cms.

Hence the most probable length is given by mean of length   4.34 cm

So, the final reading obtained for the length is 4.34 cm, but we are only sure about first digit (4) but not sure about second and third digit (0.34) due to limitation of least count of scale (0.1 cm). 

So, the significant digits will be 4 (The digits about which we are certain in the measurement) and 3(one additional digit after the digit about we are certain).

Hence, we will write length of pencil as 4.3 cm (Only significant digits) 

Rules for determining significant digits:

1. Non-zero digits are always significant. (In 123.543, all digits are significant)
2. All zeros between two non-zero digits are significant. In 123.005, all digits including zeros are significant)
3. Zeros to the left of the first non-zero digit are not significant.                                                    

(In 0.01234, Only 1,2,3 & 4 are significant).

1. If decimal point is used, zeros to the right of last non-zero digits are significant.                          (In 12.500, zeros after digit 5 are also significant) 
2. If decimal point is not used, zeros to the right of last non-zero digits are not significant. (In 12500, zeros after digit 5 are not significant).
3. If the magnitude of physical quantity is written as , such that , Then the significant figure will be same as that of A.,  term will not have any significant figure.