Angle of elevation and angle of depression

Angle of Elevation

• The angle of elevation refers to the angle formed by the line of sight when it is above the horizontal line.
• It is defined as the angle made by the line of sight as it looks upward from the horizontal plane, such as when a person observes a bird flying above them. 
• This concept highlights the importance of the line of sight in determining the angle of elevation when observing objects at a higher elevation.

Angle of Depression

• The angle of depression refers to the angle formed by a line of sight that is below the horizontal line. In contrast, the angle of elevation is above the horizontal.
• This distinction helps clarify the concepts of both angles, with angle of depression consistently defined as the angle made when looking down from the horizontal.

_____________________________________________________________

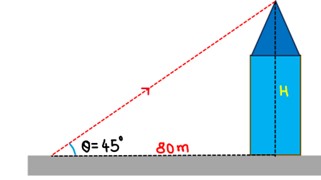
Example-1:  Height of a Church

A person observes the top of a church from a distance of 80 meters, with the angle of elevation set at 45°. To determine the height of the church.

Solution:

• We denote the height as H and utilize the definition of angle of elevation to formulate the problem. 

This scenario provides a straightforward application of the concept of angles in elevation.

Given as, 

Angle of elevation (θ) = 45°

_________________________________________________________________

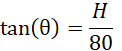
Example-2 : Height of a Building

A boy standing 48 meters from a building observes the top, making an angle of elevation of 30. Find the height of the building.

Solution: 

To find the building's height, the tangent ratio is used.

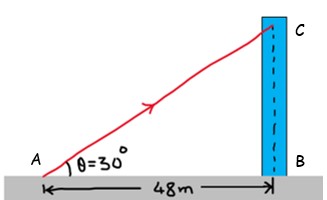
tan (30°) = height (BC) / distance (AB).

By solving the equation, 

BC= AB x tan(30°)

BC=48 / √3 meters.

It is determined that the height of the building is 48 / √3 meters.

________________________________________________________________

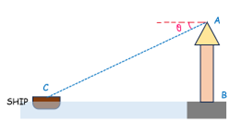
Example-3: Distance of a Ship from a Lighthouse

An observer atop a 90-meter lighthouse looks at a ship, making a 60° angle of depression. Find the distance of ship from light house.

Solution: 

Angle of depression θ=60°

Using trigonometry and the relationships in triangle ABC, 

We have,

Also, 

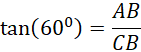
meter